Tetris Cube Solved (ALL 9,839 solutions)

Of the 12 puzzle pieces, 10 may be rotated into 24 possible orientations, and 2 may be rotated into 12 possible orientations. This means there are 24¹⁰x 12² = 9,130,086,859,014,144 (over 9 quadrillion) possible piece orientation combinations to try. The pieces may also be fitted, or 'tiled', into the 4x4x4 cube in 12! = 12x11x10x(...)x2x1 = 479,001,600 possible piece ordering permutations. The product of these numbers is 4,373,326,213,606,749,398,630,400 (over 4 million quadrillion) steps to try every possible orientation of every possible piece order permutation!

Because the cube is a rather snug 4x4x4 box there are many piece orientations that simply will not fit into the box with other pieces in their own various orientations, as anyone who tries to manually assemble a Tetris cube knows from personal experience! Consequently, the number of permutations and therefore the number of piece orientations to attempt to tile into the box are drastically diminished. For example, the initial piece order is 0,1,2,3,4,5,6,7,8,9,10,11. The next is 1,0,2,3,4,5,6,7,8,9,10,11 and then 2,0,1,3,4,5,6,7,8,9,10,11 etc. When the permutations are fully exhausted the piece order is, finally, 11,10,9,8,7,6,5,4,3,2,1,0. For the initial permutation, say pieces 0 and 1 are already in the box but none of the orientations for piece 2 fit. For this example, that would indicate 12!/(12-10)! = 239,500,800 permutations are immediately eliminated from having to be attempted, multiplied by the number of possible orientations for each of those pieces in all those discarded orientations. This can happen at any stage of the search, so the search space is in practice vastly smaller than the 4 million quadrillion figure above, bringing it into reach of a software program.

Of the 479,001,600 possible piece ordering permutations only 236,136 produce a completed cube (see below, Search Results). This means you have about 1 chance in 2,028 that a random lineup of the pieces can be put into a cube. No wonder it's not so easy! The Tetris cube is therefore about 6.7 times easier than the Bedlam cube, for which you have about 1 chance in 13,523.

Each of the 12 pieces is arbitrarily assigned a unique number, 0 to 11 (photo below). The software encodes the 3-dimensional coordinates of each cube of each piece, and then rotates them in 4 possible positions around each of the 3 axes (x,y,z) to generate every possible unique orientation and build a quick reference lookup table. The piece order permutation order is initialized to 0,1,2,3,4,5,6,7,8,9,10,11 and the orientations of each piece are reset. A 4x4x4 3-dimensional box is encoded and the initial empty cube is scanned starting at (x,y,z) coordinates (1,1,1).

The first orientation of the first piece in the permutation is fitted (or not) into the box. If it doesn't fit, the next orientation is tried, etc. If the piece fits, the next empty cube in the box is scanned along the x-axis, then y-axis, then z-axis. If the next empty cube is isolated, the last piece orientation fitted into the box is removed and its remaining orientations are tried. If the next empty cube is not isolated, the next piece in the permutation order is attempted the same way. If none of the orientations of a piece fit into the box without isolating the next empty cube, the piece order permutation is advanced so the next piece in the ordering becomes the next piece to try, and it's first orientation is attempted, etc.

By repeating this process, literally every possible orientation of every possible ordering of pieces is visited by my search software program, an undeniably rigorous method. This method will produce multiple rotated copies of each unique solution, so a further step in the program spins the solved cube around each axis and compares each rotation with a catalog of saved solutions. Only new unique solutions are then added to the catalog as the permutation sequence progresses, guaranteeing the correct catalog is produced.

Research consulting for machine learning is a specialized research service where experts apply their research skills and technical knowledge to any type of research task. It includes consulting on research projects, conducting research studies, preparing research papers, and providing feedback on research papers. The experts use data analysis techniques such as statistical methods, machine-learning algorithms, and natural language processing (NLP) to analyze vast amounts of data in order to find useful insights. For example, they can help with do my paper tasks by providing detailed feedback on the structure and content of the paper. Research consultants are highly qualified professionals who combine scientific knowledge with excellent communication skills in order to deliver optimal solutions that meet the specific requirements of customers.

Research consulting for university students is an essay service that provides in-depth guidance and professional advice on any academic research project. It helps students to formulate the right questions, develop their skills in problem solving, and conduct research effectively to get the best results. Through personalized help, research consultants can assist with essay writing, thesis preparation, data collection and analysis, and help make sure the student’s research stands out from their peers. With a strong focus on developing quality research proposals and completing tasks efficiently within set timelines, university students can benefit greatly from working with experienced professionals in this field.

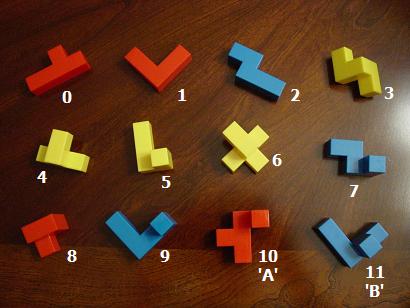Photo of the 12 Tetris Cube pieces
and the arbitrary numbers 0 to 11 assigned to each in the software program and solutions catalog.

Pieces 0 to 9 are labeled by their own numbers but 10 and 11 are labeled A and B, respectively, in the solutions catalog.

Piece 0 has 5 cubes, labeled red 'y'
Piece 1 has 5 cubes, labeled red 'V'
Piece 2 has 5 cubes, labeled blue 'z' or 's'
Piece 3 has 5 cubes, labeled yellow 'squiggle'
Piece 4 has 5 cubes, labeled yellow 'bent-T'
Piece 5 has 5 cubes, labeled yellow 'L-bump'
Piece 6 has 6 cubes, labeled yellow 'bent-X-plus'
Piece 7 has 5 cubes, labeled blue 'squiggle'
Piece 8 has 5 cubes, labeled red 'P-bump'
Piece 9 has 6 cubes, labeled blue 'V-bump-end'
Piece 10 has 6 cubes, labeled red 'F-bump'
Piece 11 has 6 cubes, labeled blue 'V-bump-edge'

Exactly 9,839 unique solutions were found. Because of rotational symmetry my software actually assembled 24 x 9,839 = 236,136 cube solutions but it discarded exactly 226,297 duplicates as 23 additional rotational copies of each unique solution. The software search completed in 43 hours on my old 2 GHz Pentium 4 laptop. The 9,839 unique solutions, however, were found within the first 21 hours and the remaining 22 hours completed permutations that resulted in rotational copies. The search space was, as expected, enormously reduced to a 'mere' total of exactly 99,432,763,039 (99.4 billion) piece order permutations visited, including dead-end orientation paths. The program attempted to fit pieces into the box exactly 2,177,206,872,576 (2.2 trillion) times and succeeded fitting them exactly 38,631,093,159 (38.6 billion) times. Indeed, 2.2 trillion is MUCH smaller than 4 million quadrillion!

Below is the software's startup analysis, the first 3 of the entire solutions catalog, and the search conclusion outputs, rigorously determined using 'brute-force' combinatorial techniques (color added for web page annotation). Pieces are mapped to numbers 0-11 and their identification is aided by the descriptive cube counts, colors and labeling in agreement with the photo above. The solutions are given in layers of the 4x4x4 box, with the top layer of the cube on the left and ending with the bottom layer on the right. Pieces 0 to 9 are given in the solutions by those numbers, and pieces 10 and 11 are given as A and B, respectively.

It takes a bit of visualization to see the pieces in the printed solutions and it helps to refer to the photo above. In Solution 1 below pieces 9 and 0 are outlined and in Solution 2 the same piece 9 is outlined. Particularly challenging to visualize are pieces spanning cube layers, such as piece 9 (blue 'V-bump-end'), which in the outlined example in Solution 1 has the 'bump' on the end of the 'V' in the top layer next to the A cube and the piece drops down the top right corner of the second layer into the third layer, where it goes to the left along the back edge of the cube. More easy to see is piece 0 (red 'y') in the bottom layer at the right of Solution 1, laid flat with the bump of the 'y' in the same layer, and piece 9 in Solution 2, where it is mostly flat within the top later and the single drop-down 'bump' cube in the next layer below. Get out your Tetris cube and try it... it's rather easy once you get the hang of it.

Download the program tetriscube.exe, a simple console application without buttons or windowing and its 700 lines of C language source code file tetriscube.c, in TetrisCubeSolved.zip. Run it yourself! Every 1,000,000 piece order permutations are output to the console screen. Email me at the address at the bottom of the page and tell me the kind of computer you used and how long it took to run. With a few trivial tweaks this code determined all 480 unique solutions of Piet Hein's Soma cube puzzle in 10 seconds (note: this linked reference cites only 240 unique solutions), both unique solutions of Hugo Steinhaus' cube in 1 second, all 19,186 unique solutions of the Bedlam cube puzzle, all 14,177 solutions of the Brother Cube, and would work for other 3D box-tiling puzzles. Note there are copyright restrictions given in the tetriscube.c source module and readme.txt files to observe regarding modification of the source code and/or re-publishing the code or output data file.

I owe this particular puzzle-solving adventure to my son Dylan, who recently challenged me to find "even one solution, daddy!" and witnessed my struggle to manually restore his Tetris Cube to its plastic box. I told him there was a way to use a computer to find every possible solution, so we encoded the cube coordinate positions of the 12 pieces on paper, and I later put that into this software over the span of a handful of days. Thank you, Dylan!

In 1986 I wrote a software program to exhaustively solve and catalog all solutions of the 2-dimensional pentomino puzzle, to the later delight of Stanford Professor Emeritus Donald Knuth, which has tens of thousands of solutions in various box dimensions (3x20, 4x15, 5x12, 6x10 and 8x8 with several 2x2 hole positions) even after sifting out reflected and rotated copies. I also have over a decade of experience creating and running supercomputer-capacity research projects so I was fully prepared to organize any "heavy duty processing power" required to catalog all the solutions and verify their number as claimed by the Tetris Cube's creators, but a laptop computer was enough.

Tetris Cube Solved ALL 9,839 Solutions

Tetris Cube Solved
ALL 9,839 Solutions