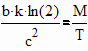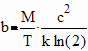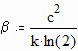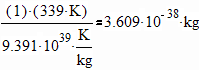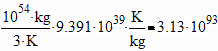Mass of 1 bit

Derivation of the mass of 1 bit of information (a binary 1 or 0) at a certain temperature,
the number of bits in a cool glass of water, plus some wild speculations on dark energy.

How can "mere information" have mass? Energy is required to partition a system into a two-state binary system (Landauer, 1961). More states for trinary, quaternary, etc., are possible using higher energies, but since all computable systems are equivalent (Church-Turing, 1936) and binary is minimally enough to compute things, we will stick with binary state systems using the lowest necessary energy. Energy has mass (Einstein, 1905), so a bit must have mass, and the hotter a bit's environment, the more mass it has. Introduced below is a new cosmological constant, which I've labeled the "thermal bit density" constant of the Universe. If you find an error please send me a note about it.

Derivation

Here is derived the relationships between binary information, mass and temperature.

UNITS
unit	symbol
bits	b
entropy	S
energy	E
temperature (°K)	T
mass (kg)	M
distance	m
time	s

CONSTANTS
description	symbol := value
speed of light
Boltzmann constant
1 mole (count)
"thermal bit density" constant (derived herein)

A bit is a binary state, 1 or 0, True or False, Up/Down, Cool/Boring, etc.

From Landauer's Principle using the laws of thermodynamics, the energy of a base-2 (binary) bit is at least

So let's take the minimum energy. Energy is system entropy times temperature, so the entropy per bit is

From Einstein's equivalence:

Remember, in the strict formulation it's an inequality:

Solve for the maximum number of bits in a given Mass at a specific Temperature:

where we can see a bit of information is literally dimensionless (in terms of physical properties of mass, temperature, distance, and time), from which we can introduce a definition for a "thermal bit density" constant in degrees K per kg, as:

Therefore, we now have the maximum number of bits in a mass at a certain temperature, and the minimum mass of a certain number of bits at a certain temperature:

and where

Mass of 1 Bit in a Hot Computer

The mass of one bit in a hot computer at 150°F (339°K) is therefore at least 3.61x10^-38 kg:

Note that as the temperature increases, so does the mass of a bit.

Number of Bits in a Cool Glass of Water

How many bits, at most, can be stored in a cool 50°F (283°K) glass of water? Since a cup of water is 0.2366 kg, it holds at most 7.85x10³⁶ bits!

Wild Speculations on the Universe, Bits of Information, and Dark Energy

Now for some wild speculations on the nature of the universe, its mass, temperature, expansion and information content in bits.

The formulations above show that as the temperature of a bit decreases, so does its mass, and vice versa. Since the universe is expanding, its volume is increasing and therefore its total possible surface area must also be increasing. The universe is also cooling as it expands, now down to only 3°K. The temperature change is directly related to the expansion of the universe, a well-known relationship.

Leonard Susskind's restatement of Gerard t'Hooft's Holographic Principle [Wikipedia, Science Daily] holds that the surface area of a system having an event horizon encodes all the states of that system. If this Principle is true, the universe therefore because of it's expansion and increasing event horizon surface area must be developing an increasing number of bits of information on its surface.

This is consistent with the requirement that as temperature decreases the mass of a bit is lower, and for a universe having a (say) fixed total mass, the formulations derived above require that number of bits within it must necessarily increase. We could just as easily assert that the development of information states within the universe and its cosmic expansion are part of the same process.

It appears that about 70% of the energy driving the universe's expansion is "dark energy" having no known source. It's obvious from the derivations shown above in combination with the Holographic principle that the accumulation of bits of information in the universe might be considered a candidate source of this dark energy, and that number of bits is literally astronomical! That is, the universe is computing itself larger at an accelerating pace as its entropy decreases.

Values for the mass of the universe (found by Google search) range between about 3x10⁵² kg and 1.6x10⁵⁵ kg, so let's use M = 10⁵⁴ kg.

This yields an information content of the entire universe of about 3x10⁹³ bits, about one ten-millionth of a google-bit (10¹⁰⁰ bits)!

Last updated 28 August 2009